某公司准备在门口铺设地毯,台阶的长为13米,高为5米,宽为5米。地毯需要覆盖台阶的踏面和踢面。每个台阶的踏面和踢面组成一个矩形,其对角线长度即为台阶的长13米,高度为5米。根据勾股定理,可计算出踏面的水平投影长度:√(13² - 5²) = √(169 - 25) = √144 = 12米。因此,每个台阶的踏面水平长度为12米,高度为5米。台阶的宽度为5米,所以每个台阶的踏面面积为12 × 5 = 60平方米,踢面面积为5 × 5 = 25平方米。每个台阶的总覆盖面积为60 + 25 = 85平方米。由于台阶只有一个(题目中未指定多级台阶,假设为单级),因此总共需要购买的地毯面积为85平方米。
计算台阶地毯铺设面积
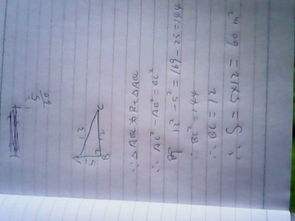
更新时间:2025-11-06 21:51:25
如若转载,请注明出处:http://www.huabangcarpet.com/product/246.html
PRODUCT
产品列表









